OPOD Inverted Mountain Shadow

Last updated on September 16, 2023

OPOD Inverted Mountain Shadow: A Fascinating Atmospheric Phenomenon

Have you ever witnessed a peculiar optical phenomenon where a mountain casts an inverted shadow into the sky? This mesmerizing display, known as an inverted mountain shadow, is a captivating sight that occurs under specific atmospheric conditions. In this article, we will delve deeper into this phenomenon and explore the factors that contribute to its occurrence.

The Enigmatic Shadows of Mauna Kea, Hawaii

One remarkable example of an inverted mountain shadow was captured by Andrew Cooper of the Keck Observatory in Hawaii. The photograph showcases the majestic Mauna Kea, casting a conventional dark blue triangular shadow with its point upwards, enveloping the smaller 2400m volcano, Hualalai. However, what makes this image truly extraordinary is the presence of another inverted triangle in the sky. This inverted shadow is visible only when the observer is well below the actual summit, as was the case for Andrew Cooper during his descent at dawn. His vantage point, approximately 200m below the summit, allowed him to witness this captivating phenomenon.

Visualizing the Inverted Mountain Shadow

To better understand the mechanics behind the inverted mountain shadow, let's explore a couple of visualization techniques. Firstly, it is crucial to note that Andrew Cooper was not at the summit of Mauna Kea during the observation. To illustrate this concept, imagine Mauna Kea being divided into two slices at the level where he stood. We will refer to the lower slice as 'A' and the upper slice as 'B'.

• All mountain shadows appear triangular due to perspective. Similar to parallel railway tracks that appear to converge at a point in the distance, the long, almost parallel shadow tube of a mountain recedes to a point. In reality, these shadows are much longer and only slightly tapering.
• As a result, both the shadow from slice 'A' and the shadow from slice 'B' will be triangular, albeit with different orientations. The shadow from slice 'A' is conventional, while the shadow from slice 'B' is inverted.

Another visualization technique involves imagining the upper slice of Mauna Kea as a cloud casting a shadow. This mental picture helps us understand that the shadow cast by the upper slice would converge at the antisolar point, forming an anticrepuscular ray/shadow.

The Skewed Shadows and Geometric Insights

Returning to the photograph captured by Andrew Cooper, we notice that the two shadows depicted in the image are skewed. This geometric observation provides valuable insights into the observer's position relative to the mountain center. In this case, Andrew was standing to the right of the mountain center, as indicated by the skewed shadows.

It is worth noting that when standing closer to the summit, the upper shadow may appear as a short spike rather than a triangular shape. This variation in shadow appearance adds further intrigue to the phenomenon and showcases the dynamic nature of atmospheric optics.

In conclusion, the inverted mountain shadow is a captivating atmospheric phenomenon that occurs under specific conditions. Through visualization techniques and geometric insights, we can gain a better understanding of this optical spectacle. The photograph captured by Andrew Cooper serves as a visual testament to the beauty and complexity of atmospheric optics. Next time you find yourself in the presence of a mountain at dawn or dusk, keep an eye out for the possibility of an inverted mountain shadow gracing the sky. It is moments like these that remind us of the enchanting wonders present in our natural world.

Inverted Mountain Shadow

Shadows cast at dawn by Mauna Kea, Hawaii. Taken on July 20, 2010 by Andrew Cooper of Keck Observatory. ©Andrew Cooper, shown with permission

A �conventional� dark blue triangular shadow with its point upwards extends from the mountain and envelops the smaller 2400m volcano, Hualalai. In the sky is another inverted triangle. �This appears only when the observer is well below the actual summit, I saw it while driving down from the summit at dawn, thus the shadow is both projected into the haze below, and seen cutting through a layer of haze and thin cloud above. I was located about 200m below the summit.�

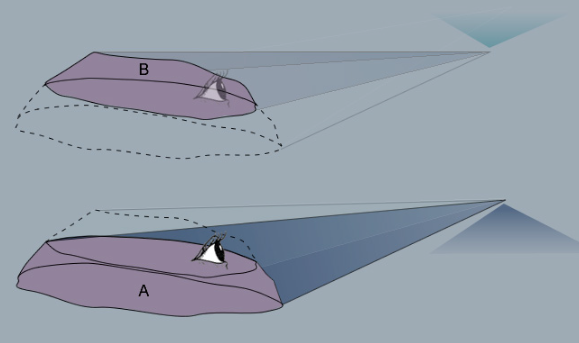
There are several ways to visualize what is happening.

The key point is that Andrew was not at the summit.

Imagine Mauna Kea sliced into two at the level where he was standing. Now take away the upper slice to leave only the lower one 'A'.

All mountain shadows appear to be triangular regardless of their profile because perspective makes the long almost parallel shadow tube recede to a point just as parallel railway tracks do. In the diagram the shadow is shown greatly foreshortened to get it on the page, in reality is very long and only slightly tapering.

If all mountain shadows are triangular, that of the lower Mauna kea slice 'A' will also be triangular as shown.

Now image there is only the upper slice 'B'. The situation is the same except to the observer the mountain is upside-down. It casts an upside down triangular shadow into the sky.

Another way of picturing the event is to imagine that the upper slice of Mauna kea is a cloud casting a shadow. It will form an anticrepuscular ray/shadow converging at the antisolar point.

An additional twist is that the two shadows in the image are skewed. The geometry tells us that Andrew was standing to the right of the mountain centre as shown.

When rather closer to the summit, the upper shadow can appear as a short spike.

Note: this article has been automatically converted from the old site and may not appear as intended. You can find the original article here.

Reference Atmospheric Optics

If you use any of the definitions, information, or data presented on Atmospheric Optics, please copy the link or reference below to properly credit us as the reference source. Thank you!