Why do we see rainbows? - The Sky Transform - OPOD

Last updated on September 16, 2023

Why do we see rainbows? - The Sky Transform

Rainbows are a captivating and beautiful phenomenon that has fascinated humans for centuries. But have you ever wondered why and how rainbows form in the sky? It turns out that the answer lies in the intricate process of light scattering and reflection by raindrops in the atmosphere. In this article, we will delve into the science behind rainbows and explore the concept of the "sky transform" that allows us to see these colorful arcs of light.

The Magic of a Single Raindrop

A single raindrop may seem insignificant, but it plays a crucial role in creating a rainbow. When sunlight passes through a raindrop, it undergoes a series of interactions that result in the formation of a rainbow. As the parallel sun rays enter the raindrop, they partially reflect from the opposite side and then exit towards the sun. The rays that deflect the least form a bright line, which becomes one point of the outer colored edge of the rainbow.

Uniting Raindrops to Create a Rainbow

While a single raindrop can produce a small portion of a rainbow, it takes millions of raindrops working together to create the full arc of colors that we observe in the sky. Each raindrop contributes its own speckle of color, but how do these individual speckles combine to reproduce the pattern of light from a single raindrop? This question extends beyond rainbows and applies to other atmospheric optical phenomena like halos, glories, and even diffraction patterns formed by ice crystals and cloud droplets.

The Concept of the Sky Transform

To understand how individual raindrops contribute to the formation of a rainbow, let's consider an abstract particle that scatters sunlight in the shape of a capital letter "L." This hypothetical particle scatters three rays labeled 'a,' 'b,' and 'c.' By imagining a cloud filled with these magical particles at varying distances, we can observe how they interact with our perception.

A cyclopean observer with a single eye would see glints of light from the particles that align with their line of sight. For example, particle '1' scatters ray 'a' towards the observer's eye, creating a bright glint in the corresponding direction. Similarly, particle '2' scatters ray 'b,' and particle '3' scatters ray 'c,' resulting in additional glints. However, the millions of other particles in the cloud remain dark to the observer's eye since their scattered rays do not reach the eye.

Generalization to Atmospheric Optical Phenomena

The concept of the sky transform applies not only to rainbows but also to a wide range of atmospheric optical phenomena. Any scattering pattern or light distribution created by a single raindrop, droplet, ice crystal, or dust particle can appear in the sky when there is a cloud of similar particles. The pattern appears in the opposite direction relative to the sun's rays and is inverted.

For example, the cone-shaped scattering of light by raindrops towards the sun forms the rainbow we see opposite the sun. Similarly, a cloud of droplets diffracting light mainly forwards with the sun's rays creates the corona around the sun. The complex geometric forms of Parry arcs, on the other hand, result from a cloud of peculiarly oriented ice prisms.

The Fascinating World of Atmospheric Optics

The study of atmospheric optics is a captivating field that unravels the secrets behind the mesmerizing phenomena we witness in the sky. By understanding how individual particles interact with sunlight and combine their scattered rays, scientists can explain the formation of rainbows, halos, glories, coronae, and various other optical displays.

Next time you marvel at a rainbow stretching across the sky, remember that it is the collective effort of countless raindrops coming together to create this awe-inspiring spectacle. The sky transform allows us to witness the beauty of nature's optical symphony and provides a glimpse into the intricate workings of light in our atmosphere.

Why do we see this?~ Reddened sunset bows ride high in the sky at Ektorp near Stockholm, Sweden. Image by Måns Hagberg. ©Måns Hagberg, shown with permission

A single raindrop glints light

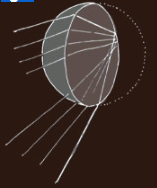
Parallel sun rays enter the drop, partially reflect from the opposite side then leave towards the sun. Those deflected least (bright line) form one point of a rainbow's outer coloured edge.

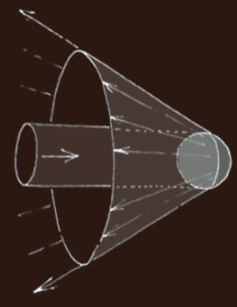
Rays entering through a ring around the drop each form a point on the rainbow. All the possible rays make a cone in the sunward direction.

The sky transform ~ Why do we see patterns in the sky, rainbows, halos, glories.. ?

A single raindrop does not a rainbow make. How does the sunward deflected light from a single raindrop transform into a huge rainbow in the sky opposite the sun? Millions of raindrops across the sky must contribute individual rainbow speckles but how do they reproduce the pattern of light from a single raindrop? The problem is actually a more general one. An individual ice crystal refracts and reflects sunlight and millions of them combine somehow to form a highly geometric halo. An individual cloud droplet forms a diffraction pattern that is somehow projected on the sky by the combined action of millions of droplets. How then is the scattering pattern of an individual droplet, ice crystal or raindrop writ large upon the sky?

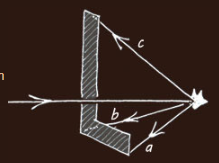
Let's look at an abstract particle that magically (we need not enquire how) scatters sun rays backwards in the shape of a capital letter "L". That is chosen not from some egomania wish for skywriting of my initial but because the symbol's extremities are defined by just three scattered rays which we can label 'a', 'b' and 'c'. Furthermore, "L" has a 'handedness', its flipped mirror image form is distinguishable from the original. Let's make a further abstraction by only considering the three extremity rays. They are sufficient because they uniquely define the "L".

L in the sky

Imagine the sky filled with a cloud of these magical particles at a range of distances. Each one of them individually scatters backwards three rays in directions 'a', 'b' and 'c'. There is no interaction between them, they all act in isolation.

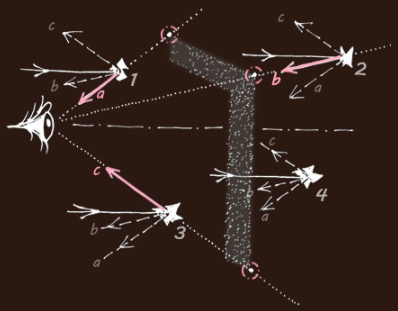
Now imagine a one-eyed, cyclopean, observer. What does the eye see? Particle '1' is so placed that its ray 'a' (and only ray 'a') reaches the eye. The eye sees a bright glint in that direction which is at a corner of the "L'. Similarly the eye sees a glint from ray 'b' scattered by particle '2'. Ray 'c' from particle '3' makes a third glint in the sky.

What about all the other millions of particles? Take one of them in an arbitrary position '4'. None of its three rays 'a','b' or 'c' reach the eye. No glint is seen. It glints its light elsewhere and might be seen by another creature but to our cyclops it is dark. Similarly all the other particles are dark.

The three glinting particles define an "L" in the sky having the same angular aspect to the eye as the scattering angles of the individual particles. There are differences. The "L" appears in the opposite direction - relative to the sun's rays - to that of the particle scattering pattern. The "L" is also inverted.

Generalisation ~ rainbows, halos, glories, coronae...

Any shaped scattering pattern or light distribution can be constructed from enough (if necessary infinitesimal) triangular elements. Therefore the demonstration above holds true for all scatterers. Any scattering pattern made by a single raindrop, droplet, ice crystal or dust particle etc will appear in the sky if there is a cloud of similar particles. The pattern appears in the opposite direction relative to the sun's rays and upside down. A single particle scattering pattern directed sunwards will appear in the sky opposite the sun, one directed forwards mainly along the sun ray direction will appear near the sun. Inverted? We do not notice that the pattern is inverted for symmetrical scattering patterns like circular rainbows, coronae and glories.

Thus we see a rainbow opposite the sun from millions of raindrops scattering light towards the sun in a cone shape. We see a corona around the sun from a cloud of droplets diffracting light mainly forwards with the sun's rays. We see the complex geometric form of Parry arcs from a cloud of peculiarly oriented ice prisms.

Note: this article has been automatically converted from the old site and may not appear as intended. You can find the original article here.

Reference Atmospheric Optics

If you use any of the definitions, information, or data presented on Atmospheric Optics, please copy the link or reference below to properly credit us as the reference source. Thank you!